Մաթեմատիկան և «Սուրբ ծննդյան տասներկու օրերը»

 

Թարգմանությունը՝ Արամ Պետրոսյանի
Խորհրդատու՝ Հերմինե Անտոնյան

Սա, իմ կարծիքով, շատ հետաքրքիր հոդված է, որում ներառել եմ երկու թարգմանություն։ Մեկը «Twelve Days of Christmas»  անգլիական սուրբ ծննդյան հին երգի թարգմանությունն է, իսկ մյուսը Թեո Դրեյնի հեղինակած մի մաթեմատիկական հոդվածի թարգմանությունն է, որը հնարավորինս լավ ընկալելու և վայելելու համար անհրաժեշտ համարեցի թարգմանել նաև բանաստեղծությունը։

The twelve days of Christmas / Սուրբ ծննդյան տասներկու օրերը
Անգլիական ամանորյա ժողովրդական երգ, որն առաջին անգամ հրատարակվել է 1780 թվականին։ Երգի շուրջ կան տարաձայնություններ, քանի որ որոշ մարդիկ պնդում են, որ այն իրականում ֆրանսիական է, սակայն, այնուամենայնիվ, պաշտոնապես՝ երգը շարունակում է համարվել անգլիական ժողովրդական երգ։

Երգի բառերի բնօրինակին կարող եք ծանոթանալ այստեղ։

Սուրբ ծննդյան առաջին օրը
Իմ իսկական սերը նվիրեց ինձ
Մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան երկրորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան երրորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Երեք հավ, երկու տատրակ
Եվ մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան չորրորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Չորս երգող ծիտիկ, երեք հավ, երկու տատրակ
Եվ մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան հինգերորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Հինգ ոսկյա մատանի, չորս երգող ծիտիկ, երեք հավ,
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան վեցերորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Ձու ածող վեց սագ, հինգ ոսկյա մատանի,
Չորս երգող ծիտիկ, երեք հավ,
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան յոթերորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Յոթ լողացող կարապ, ձու ածող վեց սագ, հինգ ոսկյա մատանի,
Չորս երգող ծիտիկ, երեք հավ,
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան ութերորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Ութ կով կթող աղախին, յոթ լողացող կարապ,
Ձու ածող վեց սագ, հինգ ոսկյա մատանի,
Չորս երգող ծիտիկ, երեք հավ,
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան իններորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Ինը պարող օրիորդ, ութ կով կթող աղախին,
Յոթ լողացող կարապ, ձու ածող վեց սագ, հինգ ոսկյա մատանի,
Չորս երգող ծիտիկ, երեք հավ,
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան տասերորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Տասը պարող լորդ, ինը պարող օրիորդ, ութ կով կթող աղախին,
Յոթ լողացող կարապ, ձու ածող վեց սագ, հինգ ոսկյա մատանի,
Չորս երգող ծիտիկ, երեք հավ,
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան տասնմեկերորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Տասնմեկ սրնգահար, տասը պարող լորդ,
Ինը պարող օրիորդ, ութ կով կթող աղախին,
Յոթ լողացող կարապ, ձու ածող վեց սագ, հինգ ոսկյա մատանի,
Չորս երգող ծիտիկ, երեք հավ,
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։
Սուրբ ծննդյան տասներկուերորդ օրը
Իմ իսկական սերը նվիրեց ինձ
Տասներկու թմբկահար, տասնմեկ սրնգահար,
Տասը պարող լորդ, ինը պարող օրիորդ, ութ կով կթող աղախին,
Յոթ լողացող կարապ, ձու ածող վեց սագ, հինգ ոսկյա մատանի,
Չորս երգող ծիտիկ, երեք հավ,
Երկու տատրակ և մի կաքավ՝ թառած տանձի ծառին։

Անկեղծ ասած, ինձ թվում է դուք հիմա մտածում եք «Այս ինչ ապուշ երգ է, ինչ հավես են ունեցել անգլիացիները, որ սենց տափակություն են երգել»։ Իրականում ոչ թե երգն է ապուշ, այլ երգի թարգմանությունը։ Բնօրինակը բավական լավն է, կարող եք այստեղ լսել և համոզվել, բայց իմ թարգմանությունը, կարծում եմ, այնքան էլ հաջող չէ։ Այնուամենայնիվ, երգը թարգմանելու նպատակը բնավ էլ թարգմանության որակով ձեզ ապշեցնելը չէր, այլ այնպես անելը, որ դուք ավելի լավ հասկանայիք հաջորդող մաթեմատիկական հոդվածի համուհոտը։

Թեո Դրեյն․ Մաթեմատիկան և «Սուրբ ծննդյան տասներկու օրերը»

Բնօրինակ

Սուրբ ծննդյան տասներկուերորդ օրը
Իմ իսկական սերը նվիրեց ինձ․․․

Քանի՞ նվեր։

Հեշտ է հաշվելը։ Պարզապես պետք է մեկից տասներկու թվերը գումարել իրար։
Հեշտ թվաց, բայց էլի՞ այդպես կանեիք, թե երգի տողը լիներ ոչ թե տասներկու թմբկահար, այլ հինգհարյուր թմբկահար։ Սարսափահար կվազեիք ձեր հաշվիչի հետևի՞ց։ Ավելի լավ ճանապարհներ կան այդքանը հաշվելու։

Եվ մի կաքավ՝ թառած տանձի ծառին։

Հինգերորդ օրը 1+2+3+4+5=15 նվերներ է տվել իսկական սերը։ Մենք կարող ենք այդ 15 նվերները վիզուալիզացնել 15 խորանարդներով՝ դասավորելով դրանք աստիճանաձև։ Ահա այսպես՝

Եթե երկու այսպիսի աստիճաններ դնենք իրար կողք, կստանանք ուղղանկյուն։ Ու աստիճանաձև ձևուկի մակերեսը կլինի ուղղանկյան մակերեսի կեսը, այսինքն՝

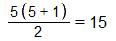
Տասներկուերորդ օրը, մենք կարող ենք նմանատիպ մի բան անել և ստանալ այսպիսի մի ուղղանկյուն, ինչպես պատկերված է նկարում։ Այդ ուղղանկյան կողմերն են 12 և 12+1=13։ Հիմա կարող ենք նաև ասել, որ՝

Ստացվում է, որ իսկական սերը Սուրբ ծննդյան տասներկուերորդ օրը նվիրում է 78 նվեր։

Իսկ քանի՞ նվեր է նվիրում իսկական սերը Սուրբ ծննդյան n-երորդ օրը։

Ելնելով քիչ առաջ ստացած հավասարումներից, մենք կարող ենք հասկանալ, որ ամեն անգամ կստանանք մի ուղղանկյուն, որի կողմերից մեկը 1-ով մեծ կլինի մյուս կողմից։ Ու աստիճանաձև ձևուկը՝ նվերների քանակը, կգտնեինք հետևյալ բանաձևով՝

Չորս տատրակ․․․

Ամեն ինչ լավ է, բայց ի՞նչ կլիներ, եթե իսկական սերը որոշեր տեղափոխվել մի այլ մակարդակ ու․․․

երկու տատրակի փոխարեն տար չորս տատրակ,
երեք հավի փոխարեն տար ինը հավ․․․
Այսինքն n քանակությամբ նվերներ տալու փոխարեն տար n * n (n-ի քառակուսի) նվեր։ Ինչպե՞ս կհաշվեինք նվերների քանակն այդ դեպքում։
Այսպես, ուրեմն տասներկուերորդ օրը կլիներ 1+4+9+25+…+144 նվեր։ Հիմա ժամանակն է՞ հաշվիչի հետևից սարսափահար վազելու։ Ոչ։
Հիմա էլ կարող ենք վիզուալիզացնել, օրինակ՝ երրորդ օրվա նվերների քանակը, այնպես, ինչպես երևում է նկարում՝

Հիմա եկեք համարենք, որ այս տարածաչափական օբյեկտը առանձին մի բլոկ է։ Եթե երկու այդպիսի բլոկ միացնենք իրար, ապա կստանանք այսպիսի մի օբյեկտ՝

Ավելացնենք ևս մի այդպիսի բլոկ ու կստանանք սա։ Աջ կողմի նկարում նույն օբյեկտը նկարված է մեկ այլ անկյունից։

Այս նկարում կարող ենք տեսնել հենց նոր ստացված օբյեկտի կրկնօրինակը, այսինքն, արդեն ունենք երկու հատ նույն այդ օբյեկտից, որոնցից յուրաքանչյուրը կազմված են երեք բլոկներից։

Միացնենք այդ երկու նույնօրինակ օբյեկտները և կստանանք այս օբյեկտը, որը վերջապես նորմալ ուղղանկյունանիստ է։

Հիմա, եկեք հասկանանք, թե որն էր այս ամբողջ բլոկների ու օբյեկտների իմաստը։ Դե, ամեն ինչ հերթով։

Եկեք պարզենք, թե քանի խորանարդ կա մի բլոկում։ Դա կարող ենք անել երկու ճանապարհով։ Առաջինը հեշտ ճանապարհն է՝ 1+4+9=14 խորանարդ։

Բայց մենք նաև ցույց տվեցինք, որ վեց այսպիսի բլոկով կարող ենք ստանալ վերջին նկարում երևացող ուղղանկյունանիստը։ Եվ ուրեմն, եկեք հաշվենք մի բլոկի խորանարդների քանակը այդ ուղղանկյունանիստի միջոցով։
Այն ունի 3 խորանարդ բարձրություն, 4 խորանարդ լայնություն և 7 խորանարդ երկարություն և կազմված է 6 բլոկից։ Կարող ենք ասել, որ ամեն բլոկում կա հետևյալ քանակությամբ խորանարդ՝

Բայց, ձեր համար միգուցե կա մի բայց։ Արդյո՞ք այս ամենը կաշխատեր, եթե մեր բլոկն ունենար ավելի շատ շերտեր, օրինակ՝ ոչ թե 3 շերտ, այլ 4 շերտ։ Մենք կարող ենք կրկնել ամբողջ պրոցեսը և համոզվել։

Վերջին նկարի ուղղանկյունանիստն ունի 4 խորանարդ բարձրություն, 5 խորանարդ լայնություն և 9 խորանարդ երկարություն, ինչպես նաև կրկին բաղկացած է 6 նույնատիպ բլոկներից։

Այս դեպքում ամեն բլոկում կա հետևյալ քանակությամբ խորանարդ՝

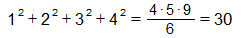
Վերջին հավասարումներին և նկարներին նայելով, կարծում եմ, կարող ենք համաձայնվել, որ վերջում ուղղանկյունանիստն ունենում է n խորանարդ բարձրություն, n+1 խորանարդ լայնություն և 2n+1 խորանարդ երկարություն։ Ու միշտ էլ բաղկացած է լինում 6 նույնատիպ բլոկից։

Ստացվում է, որ միշտ այդ բլոկի, կամ էլ քառակուսի բարձրացրած նվերների ընդհանուր բանաձևը կլիներ՝

Այսինքն մեր չափազանց շռայլ իսկական սերը տասներկուերորդ օրը մեզ կնվիրեր 650 նվեր՝

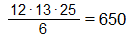
Ութ տատրակ, քսանյոթ հավ․․․

Ի՞նչ կլիներ, եթե իսկական սերն ընդհանրապես գժվեր ու որոշեր ամեն անգամ խորանարդ աստիճան ավելի շատ նվերներ տալ, այսինքն երկու տատրակի փոխարեն ութ տատրակ, երեք հավի փոխարեն՝ քսանյոթ, և այսպես շարունակ։

Եթե ուշադիր լինեք, ապա կնատեք, որ վերջում ստացված հսկայական քառակուսու մակերեսը հավասար է (1+2+3+4+5+6)^2, այսինքն կարող ենք ասել, որ՝

Դիտեք այս տեսանյութը, որտեղ տղամարդը ցուցադրում է կրկին խորանարդներով բերված մի իրավիճակ։

Եթե ուշադիր լինեք, ապա կնկատեք, որ վերջում ստացված հսկայական քառակուսու մակերեսը հավասար է (1+2+3+4+5+6)^2, այսինքն կարող ենք ասել, որ՝

Երկու հարյուր հիսունվեց երգող ծիտիկ․․․

Ինձ թվում է արդեն հոգնեցիք, այդ պատճառով էլ ես կանգ կառնեմ և կթողնեմ, որ մի քիչ գլուխ կոտրեք։ Ինչպե՞ս կհաշվեիք նվերների քանակը, եթե գլխովին խելագարված իսկական սերը որոշեր ամեն նվերից տալ 4 աստիճան բարձրացրած ավելի շատ։ Այսինքն 4 ծիտիկի փոխարեն՝ 256 ծիտիկ, 10 լորդի փոխարեն 10000 լորդ․․․